
Кольт сделал равными людей, а ракеты сделали равными флоты. На фото − пуск ПКР с ракетного крейсера проекта 58 «Адмирал Головко». Фото из архива А. Андреева
Каждый раз при попытке обосновать необходимость готовиться к войне «настоящим образом» (©В.И. Ленин), немедленно начинается набег скрытых врагов народа, утверждающих, что
«всё равно нам не сравниться с НАТО, мы не сможем выиграть такую гонку вооружений, а поэтому…»
Далее, в зависимости от личных предпочтений врага народа, предлагаются варианты в виде всеобщего ядерного суицида, безоговорочной капитуляции, отказа от ведения боевой подготовки до момента построения социализма. И так вплоть до
«вообще ничего не делать, потому что я так вижу».
Увы, но этому контингенту зачастую удаётся запутать нормальных людей. Зачастую враги народа прибегают к демагогическим приёмам типа:
«Вы не согласны на ядерный суицид? Так это значит Кац предлагает сдаться, что ли?»
Что ещё сильнее сбивает с толку нормальных людей. Поэтому, стоит разобраться с этим вопросом, дабы не давать врагам народа путать людей и дальше.
Немного о превосходстве в численности и его значении
Сразу же с порога отправим этих деятелей в нокдаун – превосходство в численности не означает превосходство в эффективности. В 1941 году в Красной Армии было намного больше танков и самолётов, нежели в вермахте и войсках союзников. Итог известен, противника пришлось гнать из-под Москвы, с берегов Волги и с Кавказских гор.
Численное преимущество совсем не всегда означает превосходство в реальных военных возможностях.
Зафиксируем первый вывод – нам нужно не численное превосходство над противником, а необходима способность разбить его. Это НЕ ОДНО И ТО ЖЕ!
Довод о том, что без сравнимой или превосходящей численности такой возможности не получить, мы ещё разберём. Пока просто зафиксируем разницу в целеполагании – вопрос о том, чтобы перегнать США и НАТО в численности сил НЕ СТОИТ. Вопрос заключается совсем в другом. И особенно это касается ВМФ.
Последней большой войной, в которой можно было решить вопрос с победой за счёт победы на море, была Русско-японская война 1904−1905 годов. В ней, кстати, в общем численное превосходство было за нами, о чём стоит помнить, но наш народ, одержимый сухопутностью и континентальностью, помнить про такое не хочет. Поэтому к этой войне мы больше возвращаться не будем, заметив лишь, что должная подготовка обеспечила бы России победу, но вместо неё был ура-патриотизм – такой же, как сегодня, без серьёзных отличий.

В Русско-японской войне начальное преимущество в численности было у русского императорского флота. Но японцы не ныли, что им не хватает сил, а просто сделали всё, что могли.
Численное превосходство оказывается решающим при более-менее равных качественных параметрах войск и сил, а также при отсутствии случайных непрогнозируемых факторов и возможности у сторон уничтожить все силы противника одним ударом за счёт огневого превосходства.
Но, надо признать, что под данным мнением (о том, что превосходство в численности носит решающий характер) имеется прочное основание. Россия вела свои самые важные войны на земле. А на суше важность численного превосходства всё же бесспорна. И перекрыть этот ресурс военным искусством получается далеко не всегда.
На море численное превосходство тоже играло свою роль. Но с поправкой на примеры типа Русско-японской. Война на море несоизмеримо сложнее войны на суше. Исход боёв в ней зависит от куда большего числа факторов, нежели на земле. И поэтому там, что называется, бывают варианты (хотя они и на суше случаются так же).
Но, тем не менее, длительное время при прочих равных условиях (сравнимая техника и уровень подготовки) именно количество вымпелов определяло суммарную мощь флотов и соотношение сил между ними.
Сейчас, однако, это не так. Для того, чтобы понять почему, разберём несколько базовых математических моделей, использовавшихся в прошлом в военном планировании.
Уравнения Чейза-Осипова-Ланчестера
Сначала о тех временах, когда количество решало почти всё.
В 1902 году лейтенант ВМС США Чейз, служивший в военно-морском колледже в Ньюпорте, вывел свой квадратичный закон, позволявший описать то, сколько сил останется у сильнейшей в сражении стороны, после того как слабейшая сторона будет уничтожена полностью. Чейз сразу же выводил свои расчёты для военно-морских сил, измеряя всё в кораблях и выстрелах орудий. Вот как выглядело самое первое аналитическое выражение, позволявшее хоть как-то математически оценить боевую силу военно-морских сил.
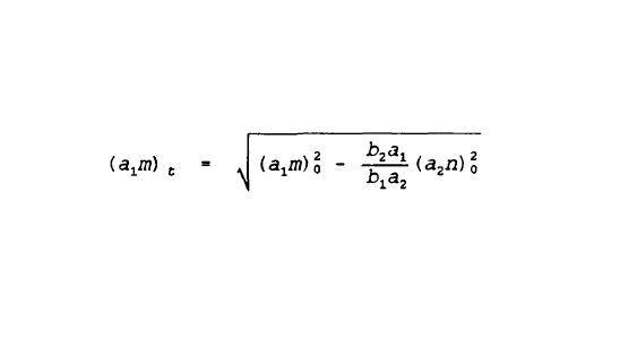
m: Число кораблей на стороне М
n: Число кораблей на стороне N
a1: Живучесть стороны М, попаданий (выстрелов)/корабль
a2: Живучесть стороны N, попаданий (выстрелов)/корабль
b1: боевая мощь стороны М выстрелов/корабль
b2: боевая мощь стороны N выстрелов/корабль
При расчётах все попадания и выстрелы считаются как единица измерения «выстрел/корабль».
Начало ХХ века было временем веры в безграничные возможности человеческого разума. В то, что наука уже почти объяснила мироздание. А, следовательно, и происходящие в мире процессы могут быть описаны математически – все.
Такие неизмеримые категории, как воинское искусство, военная хитрость, да даже простая удача в те годы считались чем-то второстепенным. Чем-то таким, что может где-то когда-то сыграть свою роль, но скорее всего не сыграет. Исключения, конечно, были. Но в основном эти вещи в расчёт не принимались. Всё решали цифры.
Позже, в ходе Первой мировой войны, квадратичные законы войны на истощение независимо друг от друга открыли русский генерал Михаил Павлович Осипов (1915) и английский математик и инженер Фредерик Ланчестер (1916), теперь уже для сражений наземных армий. Масштабы мясорубки в Европе к тому моменту вполне позволяли игнорировать всё, что нельзя было измерить числами. И неожиданно оказалось, что если рассматривать бой изолированно и упрощённо (два отряда или соединения известной силы ведут бой без подкреплений до полного уничтожения слабейшей стороны), то его исход вполне моделируется соотношениями:
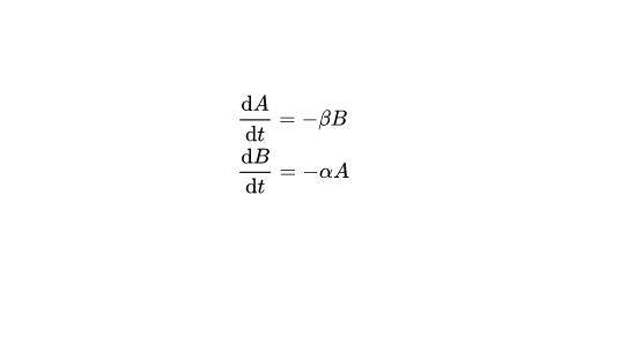
где
А - сила одной из сторон (например, число бойцов)
В - сила второй стороны
α - коэффициент боевой силы каждой единицы А (например, одного стрелка)
β - то же самое для В
В развёрнутом виде можно посмотреть здесь, с решениями для разных задач.
В дальнейшем эти уравнения непрерывно совершенствовались – добавлялась возможность оценить влияние подходящих подкреплений, внезапности атаки и многое другое. На всё это сверху легла теория вероятности, которая помогла учесть то, что, например, снаряды иногда не взрываются. Интересующиеся найдут в интернете массу информации и смогут посчитать различные сценарии разных событий. Мы же ограничимся констатацией нескольких фактов.
Первое. Во всех случаях речь шла о длящихся во времени процессах. Так, уравнением (как видно из ссылки) можно посчитать состояние сражающихся группировок на любой момент времени между началом сражения и его концом (полная гибель слабейшей из них). А что, если процесс окажется мгновенным? Такой вопрос в те времена никто не задавал, да и не могло такого произойти.
Второе. В расчётах важнейшее значение имеет численность сил. От неё всё отталкивается. Современность внесла существенные коррективы, так современные алгоритмы требуют учитывать огневую мощь участвующих в сражениях боевых систем. А так как сражаются разнородные группировки, в которых могут быть, например, танки, системы залпового огня и вертолёты, то требуется ещё и учитывать потенциал систем оружия, приводить оценки огневой мощи любой из них к некоей эталонной величине (например, измерять мощь огня танкового батальона в залпах вертолётных эскадрилий) и т.д. Подробнее о том, как такие данные исчисляются для современного боя – здесь (pdf, учитывайте, что любое событие вероятностно, все эти моделирования носят ориентировочный и неполный характер, в том числе «по режимным соображениям»).
Третье. Во всех случаях идёт речь о моделировании боя на истощение. То есть сильнейшая сторона в течение времени боя расходует свои силы, слабейшая тоже. И так до полной гибели.
Для морского боя всё это тоже работало, пока бой представлял собой «боевое состязание сторон», составной частью которого было длительное и систематическое применение оружия силами сторон друг против друга.
Конечно, приходилось приводить к единой величине мощь линкоров и эсминцев, придумывать коэффициенты для успешных засад подлодок и неожиданных попаданий на минные заграждения, но всё это до поры до времени было решаемо. Портили картину авианосцы и, отчасти, подлодки, которые воевали разовыми и мощными ударами. Но даже на Тихом океане американская палубная авиация уничтожила только 25% всех боевых кораблей Японии, остальное сделали другие силы.
С другой стороны, если рассматривать не сражение между авианосцами, а сражение их самолётов друг с другом или с кораблями, то при правильно посчитанных коэффициентах боевой силы всё «получается»: сражение нормально моделируется, а расчёты при больших масштабах и количестве боёв будут более-менее отражать реальность.
В общем, пока бой был боем с длительным по времени огневым воздействием сторон друг на друга и низкой вероятностью полного уничтожения воющей единицы с первого выстрела, квадратичные законы работали, а численность именно самих сил (людей, кораблей, самолётов, танков, пушек) носила определяющий характер, при условии сравнимого качественного уровня. Против лома не было никакого приёма в ту эпоху. Большие батальоны и эскадры доминировали, особенно когда те, кто воевал в их составе, ещё и были лучше подготовлены и обучены (например, ВМС США отличались не только материально-техническим превосходством над японцами, но ещё и лучше воюющим личным составом).
Люди, которые искренне переживают о том, что мы не можем сравниться по численности с США и НАТО (врагов народа не считаем), просто мыслят категориями той эпохи. Они забывают про один маленький нюанс.
После Второй мировой появились управляемые ракеты. А с ними пришла совсем другая эпоха.
Мир залповой модели
Представим себе, что у нас один ракетный крейсер (например, «Тикондерога» или прошедший модернизацию «Адмирал Нахимов») с сорока противокорабельными крылатыми ракетами. К примеру, с противокорабельными «Томагавками» или «Ониксами».
А против крейсера – четыре фрегата, каждый с восьмью ПКР, не важно какими. Всего у группировки 32 ракеты.
Встаёт вопрос – как это «зашить» в уравнение, хоть по «Чейзу», хоть по «Ланчестеру» (без разницы)? Что взять за численность сил?
Корабли? Но тогда получится, что крейсер гарантированно проиграет бой: он один простив четырёх кораблей противника. Или ракеты? Тогда получится наоборот? А как учесть то, что ракеты могут быть сбиты?
И самое главное – как учесть то, кто ударил первым? Что если крейсер опередит фрегаты с нанесением удара? Как тогда быть с неблагоприятной численностью?
В сражении десятков или сотен ракетных кораблей, которое тянется сутками, квадратичный закон, наверное, применим. Но у кого есть такие флоты? И где может возникнуть ситуация длительной и затяжной битвы между ними? Реально речь шла бы о единицах кораблей, сражающихся в ударных группах. Максимум − о полутора десятках. И опять же, специфика ракетного боя работала бы и тут.
Специфика, перечисленная выше, потребовала более адекватной модели, нежели модель Чейза-Осипова-Ланчестера. И такая модель нашлась.
Сегодня её называют «залповая модель». А равенства, описывающие её – залповыми уравнениями. Длительное время эта модель, созданная американским контр-адмиралом Брэдли Фиске в 10-х годах прошлого века, была в тени ланчестеровских законов. Почему?
Всё просто. В логику залповой модели Фиске было заложено следующее – у сторон А и Б, вступающих в бой, есть некоторая исходная сила. Сам бой выглядит как обмен залпами, причём у сильнейшей стороны − и залп сильнее (для артиллерийской эры это было очень логично). При этом каждый залп приводит к тому, что сила той стороны, которая этот залп получила, теряет часть своей мощи. В конце концов, слабейшая сторона в артиллерийском бою гибнет, а у сильнейшей остаётся некая часть сил − остаточная.
Почему эта модель длительное время не становилась доминирующей?
Во-первых, залпы – штука условная. Просто смотрим огонь линкора по цели на учениях по уничтожению кораблей (SINKEX) в 1989 году. Где тут точные границы залпа?
2piJQYJdYCQ
00:00
00:00
Во-вторых, для расчётов «по Фиске» требовалось выводить некую приведённую боевую силу и использовать в расчётах её. Чем не коэффициенты в Ланчестеровских уравнениях?
Ну и в-третьих (и это самое главное), с учётом того, сколько надо было условных залпов для полного уничтожения противника, процесс становился растянутым во времени. Порядок цифр, описывающих численность залпов, оказывался довольно большим. И в итоге расчёты сражений между артиллерийскими кораблями и их отрядами по модели Фиске приводили к почти тем же результатам, что и по модели Ланчестера.
Разница была всегда, но всегда − минимальная. Фактически, речь шла о получении того же результата другим способом: с количеством условных залпов вместо времени.
А вот приход на флоты ракет всё изменил.

Ракетная эра изменила характер морского боя до неузнаваемости. На фото − китайские корабли на учениях. Фото: China daily
Во-первых, залповая модель оперирует числом залпов, а не временем. Для артиллерийской эры это было одно и то же. То есть в принципе можно было даже вывести зависимость залпов от времени. В ракетную эру ракетный залп можно рассматривать как одномоментное действие – целеуказание сформировано, цели распределены, ракетный залп сформирован, пуск. После этого через короткое время удар наносится по всем кораблям противника, по которым он распределялся. То есть дискретный процесс (типа разового ракетного удара по обнаруженной цели, после которого она уничтожается и бой заканчивается) залповая модель описывает вполне адекватно, в отличие от ланчестеровских уравнений.
Во-вторых, залповая модель делала разницу между силой (численностью) залпа и численностью единиц, ведущих бой. Это было её фундаментальное отличие.
В третьих, факт того, что сила залпа задавалась, позволял учесть её не как некую определённую величину, а как разницу между исходной силой залпа и той его «частью», которую противник может отбить, отразить. В реальности – это часть ракет в залпе, которую противник может сбить.
В итоге залповая модель внезапно оказалась несоизмеримо более подходящей для ракетных сражений, нежели любая другая. Вопрос был в том, кто её полностью адаптирует к новым реалиям.
Завершил эту работу капитан ВМС США Уэйн Хьюз (Wayne Huges), который и сейчас считается в США создателем тактики ракетных сражений в её окончательной «пока» редакции.
Как выглядят залповые уравнения ракетного боя?
Примерно вот так.

где
∆ A - изменение сил А после залпа противника
∆ В - то же самое для В
α - наступательная огневая мощь А (ПКР в залпе)
β - то же самое для В
y - оборонительная мощь А − количество ЗУР, способных поразить ПКР
z – то же самое для В
u - ущерб А, ударов/корабль, для В тот же параметр как v, определяются как
u=1/w, v=1/x, где
w - живучесть, число ракет, пропуск которых приводит к гибели любого корабля А
x – то же самое для любого корабля В
В реальности, конечно, залповая модель в таком качестве не совсем применима. В ней нет кое-чего важного – вероятностей поражения цели или отражения удара. А между тем все события на войне носят вероятностный характер.
Банальный пример. Ракета, идущая на корабль противника, может выйти из строя и упасть в воду. Или же зенитная ракета, пущенная в сторону противокорабельной, может (в силу случайного фактора) промазать.
На самом деле залповые модели, скорректированные с учётом вероятностей наступления событий и возможных подкреплений для сражающихся сторон, а также и множества других факторов – существуют. Мы к ним обращаться не будем. Потому, что нам важно понять принцип того, ЧТО реально даёт превосходство в войне на море.
Пофантазируем на тему того, как в залповой модели выглядит бой небольших корабельных ударных групп.
Модель реальности
Итак, имеем столкновение сил «Красных» и «Синих». «Красные» − бедные, денег у них нет, население меньше, чем у «синих» в пять раз (если с союзниками считать), на численное превосходство они рассчитывать не могут, и его, соответственно, не имеют. Численность сил «синих» определим как «А», «красных» как «В».
Предположим, «синие» имеют пять кораблей в боевой группе. А=5. Допустим, каждый корабль имеет 50 зенитных ракет и 20 противокорабельных (остальные ячейки «синих» заняты другим оружием).
В предельно упрощённом виде будем считать, что у любой из сторон на поражение одной ПКР уходит 2 ЗУР.
Далее решаем первое уравнение, и сразу же будем искать ответ на вопрос – КАКИМ ДОЛЖЕН БЫТЬ ЗАЛП «КРАСНЫХ», ЧТОБЫ ПОБЕДИТЬ «СИНИХ» БЕЗ ПОТЕРЬ?
Почему бы и нет, в конце концов?
Тогда у нас ∆ A = -5, то есть равно по модулю первоначальному составу кораблей «синих» (потери 100%), u примем как 0,5 (достаточно, чтобы через огонь ПВО прорвалось 2 ракеты, одна из которых будет уничтожена системами ПВО ближней зоны, вторая прикончит корабль, u=1/2), соотношение β*B мы будем определять, соответственно, остается определить y.
Считаем, что ракеты «красных» идут к цели на высоте 5 метров, со скоростью 660 м/с. Высота антенн РЛС «синих» будет 20 метров, тогда дальность прямой радиовидимости у корабля «синих» − 27650 метров. И внутри этого радиуса «синие» обнаружат идущий на них залп за 41 секунду до поражения этим залпом назначенных целей (примерно).
Берём 1 секунду на автоматическое срабатывание корабельной ПВО (у AEGIS есть такой режим, и он срабатывает именно за такое время), остаётся 40 секунд. Считаем, что все ЗУР имеют радиолокационное самонаведение, горизонтальную составляющую скорости полёта 1100 м/с, подсветка целей им не нужна, канальность комплекса − без разницы, алгоритм обстрела цели – 1 ЗУР на ПКР (примем нереальное допущение в пользу «синих» - 1 ЗУР сбивает 1 ПКР в любом случае), огневая производительность отдельно взятого корабля – 1 ЗУР в 2 секунды. То есть это даже круче, чем «Арли Бёрк».

Прорвать такую оборону очень сложно. Ракет нужно немало.
Сколько ракет при таких благоприятных условиях успеет отбить один корабль «синих»? Ответ – 13. Первая ПКР будет (?) поражена на 16-й секунде после пуска первой ЗУР, последняя − на 40-й. Соответственно, y принимаем как 13.
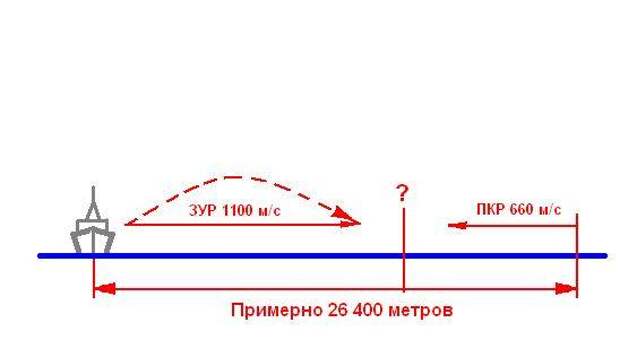
Первую секунду обороняющийся теряет на сработку системы ПВО в авт. режиме, за это время ПКР пролетит 660 м/с, потом ей навстречу выйдет ЗУР. При горизонтальной составляющей скорости ЗУР в 1100 м/с они встретятся на 16-й секунде.
А теперь просто преобразуем первое уравнение, чтобы определить искомое произведение β*B.
Итоговое равенство получается следующее:
∆ A=-(β*B-y*A)*u
-5=-(β*B-13*5)*0.5
-10=-β*B+65
или искомое β*B=75, где β – ракетный залп одного корабля «красных», а В – количество таких кораблей в атакующей группе.
Ну а дальше, как фантазия ляжет. Например, три фрегата проекта 22350 с увеличенным до 24 числом ячеек УКСК − это до 72 ПКР в залпе, максимально возможное β*B= 72. С учётом того, что на кораблях должны быть ещё и ПЛУР, то получается, что четырёх кораблей класса «фрегат» в нашей условной задаче с запасом бы хватило для уничтожения без потерь пятёрки кораблей, похожих на американский эсминец.
20 ПКР на каждом корабле просто ушли на дно, не покинув пусковых.
Теперь понятно, как это работает?
Не численное превосходство имеет значение. Имеет значение ровно одно – способность нанести удар первым, с залпом, достаточным для уничтожения противника.
Уточним вот что – это модель. И реально надо добавить, во-первых, вероятность поражения ПКР зенитной ракетой, вероятность прилёта ПКР к цели, и массу других вероятностей – каждое событие в процессе будет иметь свою вероятность наступления. Так, например, в примере выше у нас одна ЗУР гарантированно сбивала одну ПКР, что в реальных расчётах использоваться не может.
Второй момент – «красные» застигли «синих» врасплох, и отработали по ним первыми и внезапно, в результате чего смогли обойтись без потерь.
Позже Хьюз в своих уравнениях ввёл scouting effectiveness – «коэффициент разведки», учитывающий, смогли ли «красные» обнаружить и классифицировать ордер «синих» скрытно для последних, и нанести внезапный удар. Или же имел место обмен залпами до полного уничтожения одной из сторон.
Вот как это стало выглядеть.
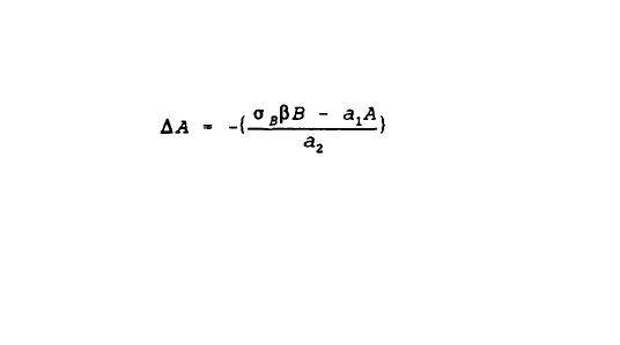
где для одной из сторон (А)
А - число кораблей стороны А
В - число кораблей стороны В
а1 - защитные возможности (число ЗУР) А, на каждый корабль
а2 - выдерживаемый ущерб, ПКР на корабль
β - наступательные возможности В, ПКР с корабля
«сигма» - коэффициент разведки
В принципе, это то же самое залповое уравнение, просто с другими обозначениями величин и «сигмой», которой в приведённом ранее уравнении не было. Если разведке атакующей стороны В удалось выявить боевой порядок А и сформировать правильное ЦУ для залпа, то «сигма» равна 1, если нет − то нулю.
Для В будет все аналогично.
Вообще же, повторимся, залповые модели с учётом вероятностей наступления событий, обеспечения/не обеспечения внезапности, эффективности разведки и т.д. – существуют.
Бывают и расчёты минимальных сил, имеющих шансы на победу против превосходящего в силах противника, а также максимальных по численности сил, наращивание которых к росту боевой эффективности уже не приводит, и многое другое.
Нам же важен вывод, который был сделан выше – гонка за паритетом по вымпелам не нужна. Те, кто отрицает необходимость вменяемого военного строительства, мотивируя это тем, что нам не догнать НАТО, либо не понимает суть обсуждаемого вопроса, либо врёт. Других вариантов нет.
А что, если мы смиримся с потерями части кораблей в атакующей группе? Тогда можно будет обойтись меньшими силами, просто придётся смириться с тем, что мы понесём потери (в реальной войне они в любом случае будут).
А если противник, имеющий численное превосходство, нас переиграет с первым залпом? Тогда ситуация переворачивается, и мы внезапно выясняем, что против лома нет приёма? Совсем нет.
Если кому-то интересно, то залповые уравнения позволяют легко «играться» с залпами – первый залп наносят А. У В осталось столько-то сил. Эти силы наносят ответный и т.д. Можно взять за B число самолётов в атаке, пересчитать для атакуемой стороны y (дальность обнаружения целей, запускаемых с самолётов по данным своих РЛС будет в разы выше, y будет тоже выше), принять за β число ракет на одном самолёте (например, 2) и т.д. Куда фантазия заведёт.
Что для слабейшей стороны важно? Кроме того, что её корабли могли отправить на цель залп требуемой численности? Внезапность.
Борьба за первый залп
В статье «Морская война для начинающих. Взаимодействие надводных кораблей и ударной авиации»был приведён один из возможных вариантов начала конфликта. Когда наши надводные корабли, ведущие слежение за океанскими группировками противника, выполняют успешный первый залп, существенно уменьшая численное превосходство противника и создавая благоприятные условия для начала систематических действий нашей базовой ударной авиации против противника. Именно обеспечение способности выполнить такой залп и есть основа морской мощи, а не абстрактная «гонка вымпелов» с США, НАТО и кем-либо ещё.
Стоит ещё раз повторить то, что писал в 1986 году Главком ВМФ СССР В.Н. Чернавин:
«Исключительно важное значение в современном морском бою приобретает такая специфическая его особенность, как возрастание роли борьбы за первый залп. Упреждение противника в нанесении удара в бою является главным методом предотвращения его внезапного нападения, уменьшения своих потерь и нанесения противнику наибольшего ущерба».
Теперь видно, как примерно это выглядит математически.
Встаёт вопрос – а как реально обеспечивать упреждение противника в залпе? Ответ – нужна разведка. Для страны с ограниченными ресурсами, что можно сказать про Россию, стоит принять за аксиому следующее правило:
Ударная мощь кораблей должна быть минимально достаточной для ослабления передовых сил противника первым залпом с минимальными своими потерями и создания условий для действий авиации. Мощь авиации должна быть достаточна для нанесения развёрнутым в море силам противника ущерба, исключающего достижение ими победы над ВМФ РФ (полное уничтожение не обязательно). А все оставшиеся ресурсы должны направляться на разведывательные силы, способные действовать в условиях военного времени.
Так, например, эта логика требует рассматривать авианосец, прежде всего как средство разведки, а уже потом – как борьбы за господство в воздухе или обеспечения ПВО корабельных соединений. Естественно, это верно для «большой войны» с превосходящими ВМС противника. В других ситуациях логика будет иная.
К созданию кораблей с управляемым ракетным оружием стоит подойти не с критерием обеспечения максимальной ударной мощи (количества ракет), а с позиций сочетания минимально достаточной ударной мощи, с максимально возможным для данного водоизмещения числом средств разведки.
Приведём пример – японские эсминцы-вертолётоносцы типов «Харуна» и «Сиранэ» при водоизмещении, сравнимом с нашими эсминцами проекта 956 (шифр «Сарыч»), несли три вертолёта.
В современных условиях это может быть сочетание из пары универсальных морских вертолётов (способных вести борьбу с подлодками, наносить удары по надводным кораблям управляемыми ракетами, осуществлять разведку с помощью своей РЛС и передавать полученные данные на корабль) и пары малогабаритных вертолётов-БЛА, применяемых чисто для разведки и занимающих столько же места, сколько один нормальный вертолёт.

Применение морских вертолётов с ракетным оружием в войне на море давно стало мейнстримом на Западе. Мы тоже должны к этому прийти.
Вторым важным условием является скорость развертывания сил. Во всех её составляющих: от скорости принятия решений до скорости хода кораблей (как экономическим ходом, так и на максимальной скорости). Скорость позволяет разбивать разрозненные группировки противника по очереди, обеспечивая превосходство в бою, включая и численное, но не имея численного преимущества в целом.
Некоторые страны это хорошо понимают. Так, японцы обеспечивают высокую скорость хода для своих боевых кораблей. Их новые фрегаты, видимо, будут иметь около 34 узлов максимальной скорости, а остальные корабли имеют тридцать или более.
К сожалению, мировые тренды на то, что скорость больше не важна, находят сторонников и в нашей стране – наши боевые корабли сегодня существенно медленнее тех, что вставали в строй тридцать или сорок лет назад. Это существенно снижает нашу способность упреждать противника в развёртывании, а, следовательно, и бороться за первый залп.
Это нужно исправлять.
Заключение
Не имея технической возможности задействовать сравнимые с противником ресурсы на развитие морской мощи и таких же, как у него технологий, нужно вложиться в организацию, оснащение и подготовку, позволяющую выиграть тот самый первый залп даже в неблагоприятных условиях, когда противник всячески пытается разорвать контакт, а в дальнейшем, в ходе военных действий, обеспечивать возможность систематического нанесения противнику тяжёлых потерь (например, силами авиации).
Не надо фантазировать про ядерный суицид. Не надо думать про то, что раз противник многочисленнее, то можно только капитулировать. В конце концов, в 1904 году перед Японией стоял именно более многочисленный противник, но не готовый настолько же к войне, с разделёнными между разными ТВД силами. Итог известен.
Нужно просто рационально подойти к предполагаемому облику военных действий ближайшего будущего, определиться с параметрами сил и средств, которые в этих военных действиях будут использоваться.
А далее просто методично и неуклонно тренироваться, готовиться к военным действиям, не упуская никаких мелочей, тщательно обдумывая каждый шаг и рационально тратя наши скромные ресурсы.
Ничего сверх этого не нужно. В том числе – не нужно для победы даже над более многочисленным противником. И это даже можно обосновать математически.
А гонка за количеством – абсолютно излишняя штука. Не только экономически неподъёмная, но и совершенно бессмысленная. Боевую мощь можно и нужно получить без неё.
И это должно быть сделано.
- Автор:
- Александр Тимохин
- Использованы фотографии:
- China Dail


Свежие комментарии